Išspręskite Kakuro galvosūkius

Šiame vadove siūlome praktinių patarimų, kaip išspręsti Kakuro galvosūkius, su sunkumais svyruoja nuo pradedančiojo iki ekspertų lygio asortimentą.

Apibendrinant taisykles: Kakuro yra dėlionė ant kryžiažodžius panašios lentos, kurioje skaitmenys naudojami tam, kad jie būtų sumuojami iki verčių, nurodytų lentos apibrėžimo kvadratuose. Be to, kiekvienos sumos grupės viduje kiekvienas skaitmuo gali pasirodyti ne daugiau kaip vieną kartą.

Tradicinis būdas išspręsti Kakuro galvosūkį yra laipsniškas: naudodami esamą lentoje esančią informaciją, galite tiksliai rasti konkrečios ląstelės vertę, kuri gali užimti tik vieną galimą vertę. Tada ta vertė užpildoma ir procesas kartojamas tol, kol atrastos visos lentos ląstelės.

Kai kuriose situacijose nėra konkrečios lentos ląstelės, turinčios tik vieną galimybę. Tais atvejais kiekviena iš galimybių turi būti ištirta atskirai ir pašalinta per prieštaravimus, kol lieka tik viena veiksmų eiga.

Buvo pateikti žemiau keletą metodų, kaip padaryti pažangą sprendžiant faktinį galvosūkį.

Unikalios sumos konkrečioms apibrėžtims

Yra keletas apibrėžimų, kuriuos galima išspręsti tik konkrečiu būdu:

suma 3 (per dvi ląsteles) visada bus 1 + 2.
suma 4 (per dvi ląsteles) visada bus 1 + 3.
suma 17 (per dvi ląsteles) visada bus 8 + 9.
suma 6 (trijose ląstelėse) visada bus 1 + 2 + 3.
suma 24 (trijose ląstelėse) visada bus 7 + 8 + 9.

ir taip toliau... Paprastai galite užveskite pelės žymeklį ant “Kakuro” tinklelio virš apibrėžimo numerio ir pasirodys įrankio patarimas, kuriame bus visos galimybės parašyti tą sumą unikaliais skaitmenimis galimų langelių skaičiuje.

Sumos, kurias galima parašyti unikaliu būdu, paprastai yra mažos sumos arba didelės sumos, kurios atsakyme verčia mažus/didelius skaitmenis, kad jas pasiektų.

Turėdami unikalų sumos rašymo būdą, padeda, tačiau turėkite omenyje, kad visos permutacijos galioja ir vis tiek turite išsiaiškinti, kurią faktinę permutaciją naudoti lentoje.

Eilutės/stulpelių apribojimai

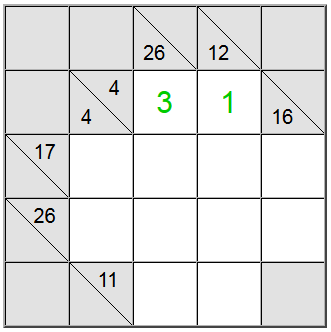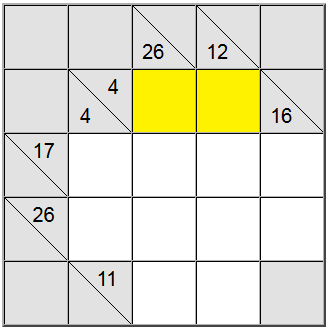
Aukščiau paryškintoms geltonosioms ląstelėms yra tik vienas sumos rašymo būdas: 4 = 1 + 3. Tačiau vis tiek turime išsiaiškinti, kurią permutaciją (1 + 3 arba 3 + 1) naudoti.

Pasirodo, kad 26 vertikalus apibrėžimas mums padeda: suma per 4 langelius, kuriuose būtų skaitmuo 1, būtų ne daugiau kaip 1 + 9 + 8 + 7 = 25. Kadangi mūsų suma yra 26, paaiškėja, kad skaitmuo 1 negali būti sumos dalis. Todėl vienintelis likęs geltonų kvadratų užsakymas yra 3 + 1.

Apibrėžimai sankryžos

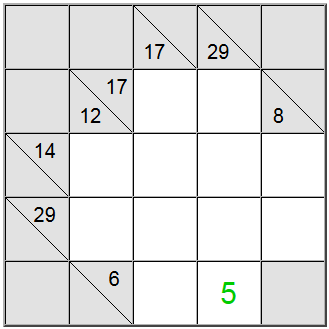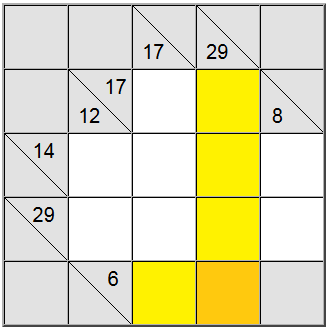
Aukščiau esančioje lentoje horizontalius geltonus kvadratus galima parašyti kaip 6 = 1 + 5 arba 6 = 2 + 4. Vertikalią geltoną sumą galima rašyti tik kaip 29 = 5 + 7 + 8 + 9.

Geltoname kvadratėlyje, randamame tų dviejų sumų apibrėžimų sankirtoje, turi būti tas pats skaitmuo, todėl horizontaliuose ir vertikaliuose apibrėžimuose turi būti bendras skaitmuo, kad jis būtų bendrinamas tarp jų. Pažvelgę į aukščiau pateiktas galimybes, galime lengvai išsiaiškinti, kad 5 yra vienintelis skaitmuo, atitinkantis šį kriterijų.

Ši technika ypač gerai veikia, kai susikerta žemos sumos su didelės sumos raiška. Mažos sumos ir didelės sumos apibrėžimai yra tie, kurie turi santykinai mažą arba didelę sumos raiškos skaičių (mūsų pavyzdyje atitinkamai 6 ir 29), palyginti su turimų langelių skaičiumi. Kadangi 6 yra santykinai mažas, tai privers mažus skaitmenis sumos vaizdavime, o 29 - didelius skaitmenis (norint pasiekti šias sumas naudojant duotą langelių skaičių). Todėl mažų ir aukštų skaitmenų sankirtoje greičiausiai bus tik vienas kandidatas faktinei langelio vertei.

Min./max vertės sumų grupei

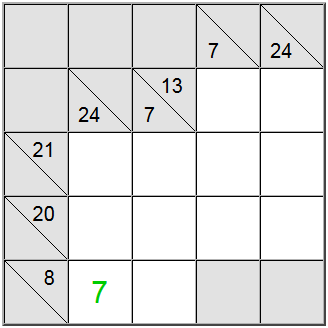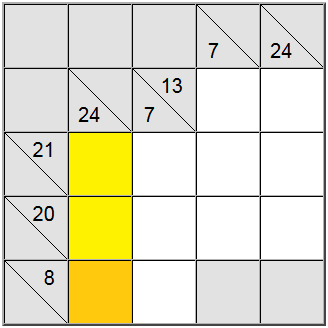
Kartais naudinga išsiaiškinti maksimalią arba minimalią sumos grupės vertę. Tai gali suteikti jums suprasti, kas galioja tos konkrečios sumos skaitmenų diapazonas, o tai savo ruožtu padės jums padaryti koreliaciją su kitais apribojimais ir išsiaiškinti unikalius priskyrimus lentoje.

Aukščiau pateiktame pavyzdyje geltonos vertikalios ląstelės priima tik vertes, lygias 7 ar didesnėms. Jei bandysite priskirti 6, galite lengvai išsiaiškinti, kad 6 + 9 + 8 = 23 todėl apibrėžimo suma 24 nebūtų pasiekiama.

Kadangi 7 yra minimumas, horizontalus apibrėžimas, turintis 8 kaip sumą, verčia 7 toje padėtyje.

Išvada

Praktika yra geriausias būdas pamatyti, kaip šis patarimas gali būti taikomas faktiniuose Kakuro žaidimuose. Žaisk galvosūkį iš tikrųjų. Linkime sėkmės ir daug linksmybių!

Žaisk Kakuro